VITEEE 2014 :: Mathematics :: General questions

• Mathematics - General questions

If the vertices  of a triangle are A(0,4,1) ,B(2,3,-1) and C(4,5,0) then the orthocentre of $\triangle ABC$ is 

Answer:

Explanation:

 Vertices of $\triangle ABC$ are A(0,4,1) ,B(2,3,-1) and C(4,5,0) 

 AB= $\sqrt{(2-0)^{2}+(3-4)^{2}+(-1-1)^{2}}=\sqrt{4+1+4}=3$

$BC=\sqrt{(4-2)^{2}+(5-3)^{2}+(0+1)^{2}}=\sqrt{4+4+1}=3$

and 

$CA=\sqrt{(4-0)^{2}+(5-4)^{2}+(0+1)^{2}}=\sqrt{16+1+4}=3\sqrt{2}$

 $AB^{2}+BC^{2}=AC^{2}$

$\therefore$  $\triangle$ ABC is a right angled triangle 

We know that  , the orthocentre of a right angled triangle is the vertex containing the right angle 

$\therefore$ Orthocentre is point B(2,3,-1)

A four-digit number is formed by the digits 1,2,3, 4 with no repetition. The probability that the number is odd, is 

Answer:

Explanation:

Given digits are 1,2,3,4

 Possibilities for units place digit (either 1 or 3)=2

 Possibilities for ten 's' digit=3

 Possibilities for hundred's place digit=2

 Possibilities for thousand  place's digit=1

 $\therefore$  Number of favourable outcomes

=$2 \times 3 \times2 \times 1=12$

 Number of numbers formed by 1,2,3,4(without repetitions)=4!

 $\therefore$ Required probability = $\frac{12}{4 \times 3 \times 2}=\frac{1}{2}$

Let X denote the sum of the numbers  obtained when two  fair dice are rolled . The variance and standard deviation of X are

Answer:

Explanation:

Ley x denote the sum of the numbers obtained  when  two fair dice are rolled

So, X may have values 2,3,4,5,6,7,8,9,10,11 and 12

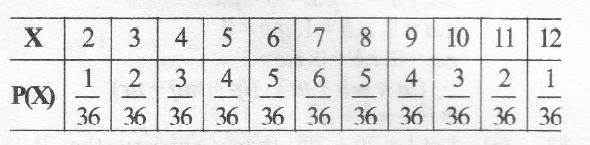
 $P(X=2)=P(1,1)=\frac{1}{36}$

 $P(X=3)=P{(1,2),(2,1)}=\frac{2}{36}$

 $P(X=4)=\frac{3}{36}$, $P(X=5)=\frac{4}{36}$

 $P(X=6)=\frac{5}{36}$, $P(X=7)=\frac{6}{36}$

  $P(X=8)=\frac{5}{36}$,

$P(X=9)=\frac{4}{36}$,$P(X=10)=\frac{3}{36}$,$P(X=11)=\frac{2}{36}$,

$P(X=12)=\frac{1}{36}$,

$\therefore$ Probability distribution table is given below

$ Mean \overline{X}= \sum XP (X)$

=$\frac{\left[2\times1+3\times2+4\times3+5\times4+6\times5+7\times6+8\times5+9\times4+10\times3+11\times2+12\times1\right]}{36}$

 $=\frac{252}{36}=7$

 Variance = $\sum X^{2} P(X)-\overline{X}^{2}$

$\frac{\left[2^{2}\times1+3^{2}\times2+4^{2}\times3+5^{2}\times4+6^{2}\times5+7^{2}\times6+
8^{2}\times5+9^{2}\times4+10^{2}\times3+11^{2}\times2+12^{2}\times1\right]}{36}$-$7^{2}$

 =$\frac{1974}{36}-49$

=$\frac{1974-1764}{36}$

$\frac{210}{36}=\frac{35}{6}$

$\therefore$  Variance =$\frac{35}{6}$

 and SD=$ \sqrt{\frac{35}{6}}$

If the integers m and n are chosen at random from 1 to 100, then the probability that a number of the form $7^{n}+7^{m}$ is divisible by 5, equals to 

Answer:

Explanation:

let I=$7^{n}+7^{m}$  , then we observe that $7^{i}$ ,$7^{2}$ ,$7^{3}$  and $7^{4}$  ends in 7,9,3 and 1 respectively. Thus , $7^{i}$  ends in 7,9,3 or 1 according as  i  is of the form 4k+1,4k+2,4k-1 respectively 

 If  S  is the sample space, then $n(S) =(100)^{2}$

$7^{m}+7^{n}$ is divisible by 5, if 

(i)  m is of the form 4k+1 and n is of the form  4k-1 or

(ii) m is of the form 4k+2 an n is of the form 4k or 

(iii)    m is the form 4k-1 and n is of the form 4k+1 or 

(iv)   m is of the form 4k and n is of the form 4k+1 or 

 So, number of favourable  ordered pairs (m,n)  =$4 \times 25 \times 25$

$\therefore$   Required probability= $\frac{4 \times 25 \times 25}{(100)^{2}}= \frac{1}{4}$

If a,b, c are three non-coplanar vectors p,q,r are reciprocal vectors , then (la+mb+nc) .(lp+mq+nr) is equal to 

Answer:

Explanation:

p,q and r reciprocal vectors of a,b and c respectively  

So , p.r=1, p.b=0=p.c

q.a=0,q.b=1,q.c-=0

r.a=0, r.b-=0,r.c=1

$\therefore$  (la+mb+nc).(lp+mq+nr)

=$l^{2}+m^{2}+n^{2}$

• Mathematics - General questions